EFHC.MX

Figura 1
Circuito a resolver

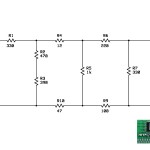
El primer paso para resolver este circuito es hallar su valor de resistencia total, es decir la resistencia equivalente del circuito. Recordemos que por mas complejo que sea un circuito, la fuente “lo ve” como si solo fuera una simple resistencia…

Tabla de valores:

• E = 5V
• R1 = 330Ω
• R2 = 470Ω
• R3 = 390Ω
• R4 = 12Ω
• R5 = 1kΩ
• R6 = 220Ω
• R7 = 330Ω
• R8 = 680Ω
• R9 = 100Ω
• R10 = 47Ω

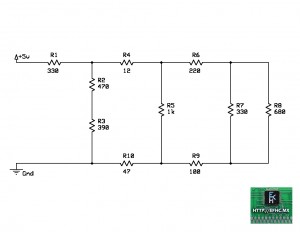
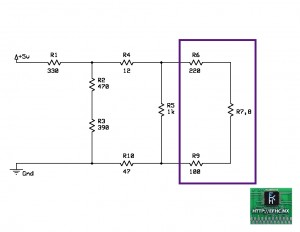
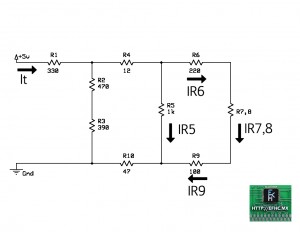
Usualmente para resolver este tipo de circuitos, se comienzan a hacer sub-circuitos desde la parte mas alejada de la fuente de alimentación. Así que comenzaremos con el circuito paralelo que forman R7 y R8.

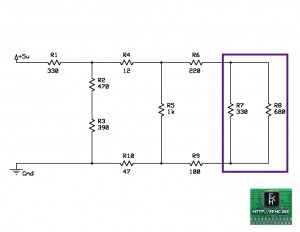
Re-ordenando el circuito, nos quedaría de la siguiente manera:

Donde R7,8 es ni mas ni menos que la resistencia equivalente del paralelo de R7 con R8.
Para saber el valor de R7,8 solo tenemos que aplicar la formula para circuitos resistivos en paralelo. La cual nos dice que:

“La resistencia total equivalente de un circuito paralelo con resistencias es el inverso de la suma de los inversos de las resistencias involucradas”

Lo anterior expresado con formulas es:

Rt = 1/((1/R1+(1/R2)+(1/R3)+…(1/Rn))

Aplicando la formula en el circuito que deseamos resolver:

R7,8 = 1/((1/R7+(1/R8))

Vaciando valores:

R7,8 = 1/((1/330 + (1/680)) por lo tanto, R7,8 = 222.18Ω
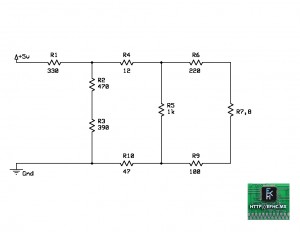
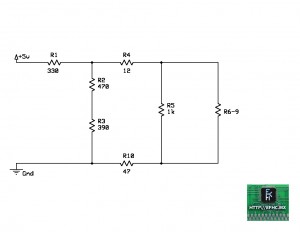
Continuando con la resolución del problema, tenemos ahora frente a nosotros un circuito serie formado por R6, R7,8 y R9.

Re-dibujando el circuito, quedaría como se muestra a continuación:

Para hallar el valor de R6-9 (resistencia equivalente del sub-circuito formado por R6, R7, R8, R9) usamos la formula para resistencias en serie, que dice:

“La resistencia total equivalente de un circuito serie con resistencias es la suma de las resistencias involucradas”

Formula:

Rt = R1 + R2 + R3 + …Rn
Aplicando la formula en el circuito que deseamos resolver:

R6-9= R6 + R7,9 + R9

Vaciando valores:

R6-9= 220 + 222.18 + 100 por lo tanto, R6-9 = 542.18Ω
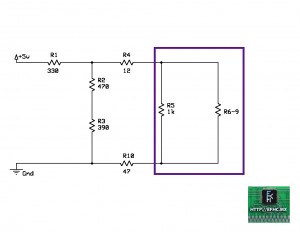
Ahora nos queda un circuito paralelo formado por R5 y R6-9.

Aplicando las formulas anteriormente vistas, tenemos que:

R5-9 = 1/((1/R5) + (1/R6-9))

R5-9 = 1/((1/1000) + (1/542.18)) por lo tanto, R5-9 = 351.57Ω

Y el circuito nos quedaría como lo muestra la siguiente imagen.

Vemos que ahora se nos formo un circuito serie entre R4, R5-9 y R10.
Aplicando la formula para circuitos serie:

R4-10 = R4 + R5-9 + R10

Vaciando valores:

R4-10 = 12 + 351.57 + 47 por lo tanto, R4-10 = 410.57Ω

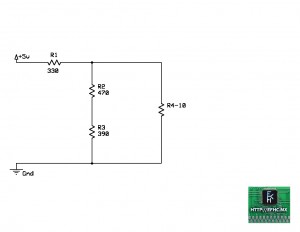
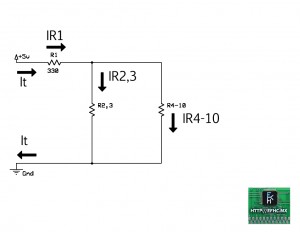
Y el circuito se reduce a esto:

Para continuar con la resolución del problema, debemos primero liberarnos de la serie que forman R2 y R3 aplicando las formulas ya conocidas.

R2,3 = R2 + R3

Vaciando valores:

R2,3 = 470 + 390 por lo tanto, R2,3 = 860Ω

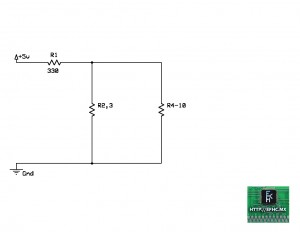
Quedándonos el circuito de la manera que se muestra en la imagen anterior.

Ahora nos queda un paralelo formado por R2,3 y R4-10, así que resolvámoslo.
R2-10 = 1/((1/R2,3) + (1/R4-10))

R2-10 = 1/((1/860) + (1/410.57)) así que: R2-10 = 277.90Ω

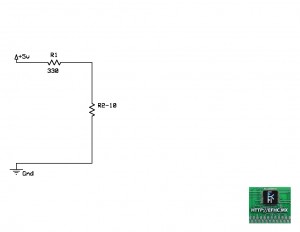
Vemos que ahora solo nos resta resolver la serie formada por R1 y R2-10, así que manos a la obra…
Rt = R1 + R2-10

Rt = 330 + 277.9

Rt = 607.9Ω

Así que ahí esta el primer paso de la resolución del problema, ya hallamos su resistencia total equivalente.
En base a eso, vamos a buscar la corriente total del circuito, es decir la máxima corriente que puede circular por el circuito. Es muy fácil, solo hay que aplicar ley de Ohm.

Formula:
It = Et / Rt así que It = 5 / 607.9 Por lo tanto:

It = 8.2mA

En base a esto podemos obtener la potencia total del circuito.

Pt = Et * It o lo que es lo mismo: Pt = 5 * .0082 entonces:

Pt = 41mW
Hallemos pues todas las caídas de voltaje en las resistencias y sus corrientes respectivas.

Ahora iremos al revés de cómo comenzamos así que por ley de Ohm y leyes de circuitos serie y paralelo obtengamos los valores.

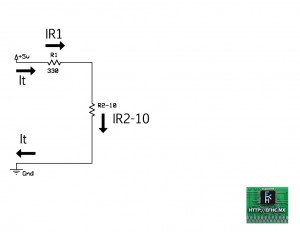
Tenemos ni mas ni menos que un circuito serie, lo mas fácil de hallar el la corriente, pues es la misma en todos los componentes en un circuito serie, así que:

It = IR1 = IR2-10 por lo tanto:
IR1 = 8.2mA

IR2-10 = 8.2mA

Aplicando ley de Ohm obtenemos los voltajes.
ER1 = IR1 * R1

ER1 = .0082 * 330

ER1 = 2.7V

ER2-10 = IR2-10 * R2-10

ER1 = .0082 * 277.9

ER2-10 = 2.28V

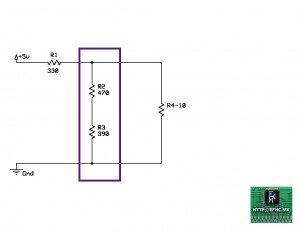
Pero R2-10 no es una sola resistencia, sino un sub-circuito, un conjunto de resistencias, tal y como lo muestra la siguiente imagen:

Podemos apreciar que R2-10 esta compuesta por R2,3 y R4-10 que también son sub-circuitos. Podemos ver que se encuentran conectadas en paralelo así que lo mas fácil de obtener son sus voltajes, que son idénticos. Por lo tanto:
ER2-10 = ER2,3 = ER4-10
ER2,3 = 2.28V
ER4-10 = 2.28V

Para obtener sus corrientes, solo aplicamos ley de Ohm:
IR2,3 = ER2,3 / R2,3

IR2,3 = 2.28 / 860

IR2,3 = 2.65mA
IR4-10 = ER4-10 / R4-10

IR4-10 = 2.28 / 410.57

IR4-10 = 5.55mA
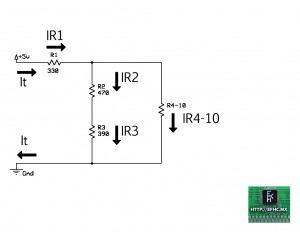
Pero, R2,3 esta realmente compuesta de R2 y R3 conectadas en serie tal y como lo muestra la siguiente gráfica.

El hecho de tener una conexión en serie nos indica que sus corrientes son iguales, así que:
IR2,3 = IR2 = IR3
IR2 = 2.65mA
IR3 = 2.65mA

Si deseamos hallar los voltajes, solo aplicamos ley de Ohm.
ER2 = IR2 * R2

ER2 = .00265 * 470

ER2 = 1.25V
ER3 = IR3 * R3

ER3 = .00265 * 470

ER3 = 1.03V

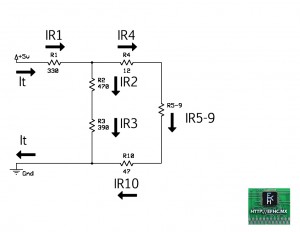
Ahora deshacemos el circuito implícito en R4-10 y nos queda como se muestra:

Al ser un circuito serie, todas las corrientes son iguales.

IR4-10 = IR4 = IR5-9 = IR10
IR4 = 5.55mA
IR5-9 = 5.55mA
IR10 = 5.55mA
Y los voltajes serian:
ER4 = IR4 * R4

ER4 = .00555 * 12

ER4 = 66mV
ER5-9 = IR5-9 * R5-9

ER5-9 = .00555 * 351.57

ER5-9 = 1.95V

ER10 = IR10 * R10

ER10 = .00555 * 47

ER10 = 260mV
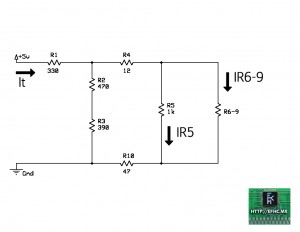
Una vez hallado estos valores procedemos a la siguiente parte del problema, o sea deshacer a R5-9

Como vemos, esta compuesta de R5 y de la asociación de resistencias R6-9. Tiene una conexión en paralelo, así que sus voltajes es lo mas fácil de hallar pues estos son iguales.
ER5-9 = ER5 = ER6-9
ER5 = 1.95V
ER6-9 = 1.95V

Y las corrientes son:
IR5 = ER5 / R5

IR5 = 1.95 / 1000

IR5 = 1.95mA
IR6-9 = ER6-9 / R6-9

IR6-9 = 1.95 / 542.18

IR6-9 = 3.6mA

Ahora desasociamos a R6-9 para que nos quede lo siguiente:

Como vemos, R6-9 esta formada por R6, R7,8 y R9 en serie. Así que:

IR6-9 = IR6 = IR7,8 = IR9
IR6 = 3.6mA
IR7,8 = 3.6mA
IR9 = 3.6mA

Obteniendo voltajes:
ER6 = IR6 * R6

ER6 = .0036 * 220

ER4 = 792mV
ER7,8 = IR7,8 * R7,8

ER7,8 = .0036 * 222.18

ER7,8 = 800mV

ER9 = IR9 * R9

ER9 = .0036 * 100

ER9 = 360mV
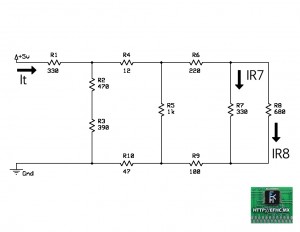
Así que por lo tanto solo nos queda resolver la ultima parte del problema. R7,8 esta compuesto por R7 y R8 conectadas en paralelo. Saquemos sus voltajes.

ER7,8 = ER7 = ER8
ER7 = 800mV
ER8 = 800mV

Y ahora sus corrientes:
IR7 = ER7 / R7

IR7 = .8 / 330

IR7 = 2.42mA
IR8 = ER8 / R8

IR8 = .8 / 680

IR8 = 1.18mA
Pues bien, con esto queda resuelto el circuito mixto serie / paralelo con resistencias.
Dudas o comentarios déjenlas al calce de este post. Gracias

Ing. Emmanuel Fernando Herrera Cortés.